BUAA-OO-第一单元:表达式展开
BUAA-OO-第一单元:表达式展开
【小女子废话较多,总是“有感而发”地“抒情”,这些不重要的话用“【】”标注出来了,可以尽情跳过~】
前言
这是本学期OO的起航,从实现的角度而言,我认为以下几种预习选择至少要有一种,否则第一周的作业会很难顺利完成:【学业是其次,主要是很毁心态哇~ 开学暴击~】
- 大二上学期OO先导课或者java课学习
- 大二寒假期间对于java语言的熟悉掌握,并且提前预习关于面向对象课程的知识点
-
PS:
个人会比较推荐OO先导课,但是名额有限,许多同学会抢不到,这种情况下,可以向该课的助教老师申请“旁听”,即与选上的同学同步学习并完成作业,但是最后不会有学分。
【小女子就是走的“旁听”这条路,但是由于个人的懒惰,我的OO先导课学习非常模糊,也导致了第一单元作业完成得比较痛苦,望引以为戒~】
第一次作业
本次作业需要完成的任务为:读入一个包含+、-、*、^、()的多变量表达式,输出恒等变形展开所有括号后的表达式。
- PS:
- 其中括号的深度至多为 1 层
- 乘方也不是用
^这样的单个符号表示,而是用的**双符号表示,这一点可以在预处理中完成替换【如果这一步不完成,问题也不大~ 小女子又又是因为懒惰并没有替换,但是,不得不承认换了之后会看着很快乐~】 - 多变量只涉及
x,y,z - 最终输出的表达式中不能含有
() - 更多要求详见教程
UML类图
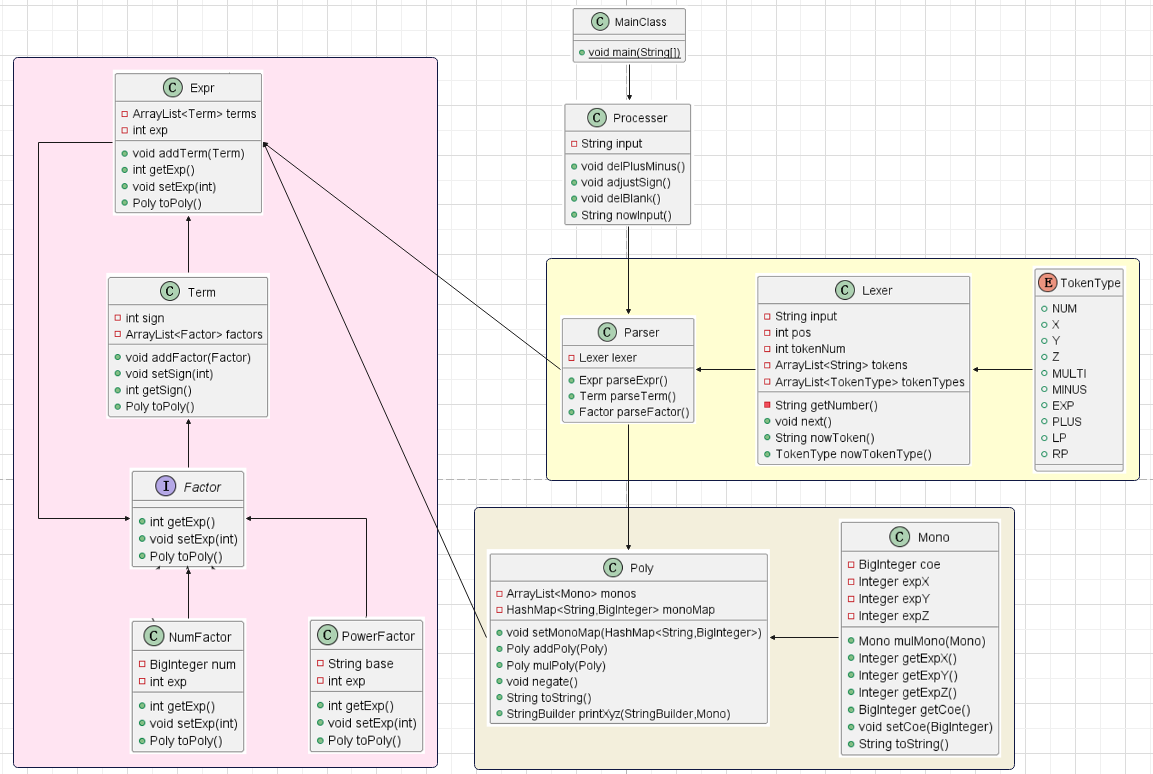
代码架构
数据结构
1 | Expr := Term | Term [+|-] Expr |
通过分析表达式,我们发现它主要包含三部分——Expr,Term,Factor,而Factor又有三种——幂函数,常数因子和表达式因子。
分析Factor时,我们发现它数据抽象层次重合度低,但是行为抽象层次重合度高,因此这里我们引入接口Factor,来方便使用Expr,NumFactor,PowerFactor:
1 | //Factor.java |
流程分析
具体如何处理并输出除去括号后的表达式,我大致分为了三个步骤——预处理、表达式解析、计算优化输出,下面进行具体分析。
预处理
为了简化之后的步骤我进行了三大类预处理——去除空格,去连续的重复的[+|-],增或减+和0:
1 | //MainClass.java |
【在( 和-之间加上0,是我debug时候发现的一种简化处理方式,又又又是为了偷懒,实在懒得思考-开头的处理方式了,个人觉得还挺好用的~】
表达式解析
有大致两种主流方法进行表达式解析,分别是递归下降算法和正则表达式算法,众所周知正则表达式算法的迭代性在“表达式解析”中比较差,为了方便于接下来的嵌套括号、自定义函数等等迭代,这里推荐递归下降算法。
【当然,通过“严刑逼供”(采访)身边的同学~ 我发现用正则表达式算法的同学很少,多数使用的递归下降算法,只是可能局部会涉及正则表达式匹配,可以认为是递归下降+正则算法。但是由于小女子又又又又懒了~ 所以没有具体询问他们是在哪一块使用的正则,因此这里仅仅简述“递归下降算法”。】
递归下降算法的主要组成部分分别是——Lexer(词法分析器)和Parser(语法解析器)。相关代码在Training和exam(第一周实验课)中有给出简单的框架,我们可以在这个基础进行修改迭代。
Lexer
在本次作业中,表达式的基本语法单元的类型有 NUM, X, Y, Z, MULTI, MINUS, EXP, PLUS, LP, RP,我们将这些语法单元的类型用TokenType这一枚举类型来记录。
【仅仅是为了方便理解,和后续“优雅化”代码,可以无需这个类。哇吼~ 又是enum呢~ 在数据结构课程中也出现过的它,小女子当时学得比较糊,这里稍微补了补知识点漏洞。】
1 | public enum TokenType { |
具体的Lexer实现如下:
1 | //Lexer.java |
Parser
Parser类的设计主要是沿用了本单元练习题中的写法,将表达式的解析分成了三部分——parseExpr(), parseTerm(), parseFactor(),每一部分的解析都遵循形式化文法。
以parseExpr()为例,因为第一项之前可能带有符号,于是我们就先将符号(+或者-)解析出来,然后解析第1项。解析完第1项后,我们就可以直接使用while循环对后面的项依次进行解析。
但是,在我的语法解析中,为了不让指数影响NumFactor,我在parseTerm()和 parseFactor()分别得到下层函数返回值之后,立刻处理乘方,将其用for循环乘起来,注意此时相乘的因子或项,都要把它们的exp(指数)设置为1。
最后结构是parseExpr()调用 parseTerm(), parseTerm()调用 parseFactor(),parseFactor()调用parseExpr()。
1 | //Parser.java |
计算优化输出
本次作业的计算单元通过分析可以归纳成式子——$$Expr = \sum a_ix^{n_i}$$
即我们可以把所有项和因子都化成单项式 ,然后用这个单项式进行计算,最终化简为多项式。因此,这里我们再建立两个类——Poly(多项式类)和Mono(单项式类)。
【强烈建议这里就不要叫它Mono了,直接叫Unit类,免得后续迭代的时候,还要一个个小心改动(虽然可以Ctrl+R直接替换,但是我担心改错,还是一个个看了),小女子已经吃过这个苦了~】
Mono
Mono类含有两个成员变量——coe和exp,分别代表系数和x的指数。然后还有toString()方法,将Mono转化成 *“系数*底数*指数” 这种形式
1 | //Mono.java |
Poly
Poly类里面,我定义了两个容器,分别是——ArrayList容器和HashMap容器,全都容纳一系列Mono,前者我用来方便输出,后者我用来方便计算。【这里没有必要设计两个容器,只是小女子脑子不灵光,总是喜欢ArrayList,但是它确实在计算时,不如HashMap好用~】
此外,还有addPoly(),mulPoly()和powPoly()等方法来实现多项式的运算。
最后,用toString()方法将解析到的Poly表达式转化为待输出的字符串形式。
1 | //Poly.java |
剩下的问题就是,如何在递归下降算法解析完表达式之后,把它全部转为Poly类型。这里,我采用在Expr、Term、Factor等类中都写一个toPoly()方法,将类中的内容转化为多项式。
【本质上也是递归下降算法,小女子听闻有一些大牛是合并了两个递归下降的,但是由于自己的笨笨和又又又又又懒懒,没有特别了解清楚。】
-
NumFactor和PowerFactor(幂函数因子)的toPoly方法很简单,直接转化为 只含有一个Mono的Poly即可。例如,因子5可以转化为一个只含有单项式5*x**0的多项式,因子x**2一个只含有单项式1*x**2的多项式。 -
Term类的toPoly()方法是:将该类中含有的所有Factor的Poly形式(即toPoly()的结果)用mulPoly()方法乘起来。1
2
3
4
5
6
7
8
9
10
11
12//Term.java
public Poly toPoly() {
//定义为1*x**0*y**0*z**0的Poly
//...
for (Factor it : factors) {
//调用multPoly()
}
if (sign == -1) {
//调用negate()
}
return poly;
} 注意一个细节,因为项是有符号的,如果该项整体是负的,我们需要把
Poly中所有的单项式的系数取反,这个取反操作我们是通过Poly类中定义的negate()方法实现的。 -
Expr类的toPoly()方法是:将其含有的所有Term的Poly形式(即toPoly()的结果)用addPoly()方法加起来。1
2
3
4
5
6
7
8
9//Expr.java
public Poly toPoly() {
//定义为0*x**0*y**0*z**0的Poly
//...
for (Term it : terms) {
//调用addPoly()
}
return poly;
} -
这样,我们就可以通过在每个类中定义的
toPoly()方法自底向上地得到表达式的多项式形式。最后,我们再通过Poly中的toString()方法就可以获得最终展开后的结果。即先expr.toPoly(),再poly.toString()。- PS:一些输出时优化性能的小方法:
- 如果单项式系数为
0,则最终结果为0, - 如果单项式系数为
1,则可以省略系数,简化为 - 如果单项式系数为
-1,则可以省略系数,简化为 - 如果单项式x的指数为
0,则最终结果只输出系数 - 如果单项式x的指数为
1,则指数部分可以省略,简化为 - 如果单项式x的指数为
2,则x**2可以化简为x*x
- 如果单项式系数为
- PS:一些输出时优化性能的小方法:
第二次作业
本次作业需要完成的任务为:在上一次作业的基础上,增加嵌套多层括号,新增三角函数因子、自定义函数因子,共三项任务。
【虽然看上去不多,但是小女子智商有限,迭代和debug的实际时间,比第一次作业“从无到有”编写代码的时间还长。只能说自己对于java的理解还是很浅显,尤其卡我的bug是——深拷贝、HashMap的重写equal()和hashCode(),以及一个一个疑惑“为什么我的代码调试结果和运行结果不一样呢?”】
- PS:
- 三角函数括号内部包含任意因子
- 自定义函数的函数表达式中不会调用其他函数
- 自定义函数只有
f、g、h三个名字 - 更多要求详见教程
UML类图
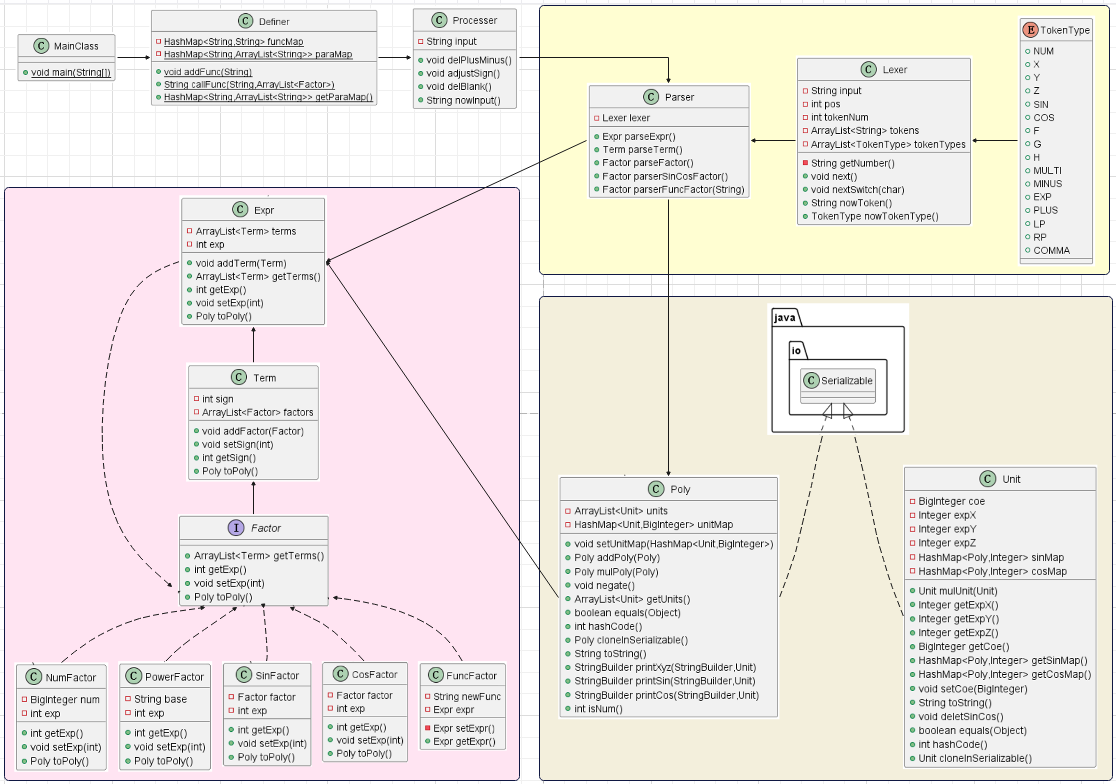
代码架构
数据结构
1 | Expr := Term | Term [+|-] Expr |
通过分析表达式结构,我们发现可以给Factor新增两种类——三角函数因子,自定义函数因子:
三角函数因子
由于题目限制,我们可以只要新建sinFactor类和cosFactor类(其实也可以合并为一个类),类中有两个成员变量——factor(表示三角函数括号内的因子),exp(表示三角函数的指数部分):
1 | //SinFactor.java |
自定义函数因子
为记录并调用自定义函数,我新建了两个类——数据类FuncFactor、工具类Definer:
FuncFactor
FuncFactor类的成员变量有——newFunc(/将函数实参带入形参位置后的字符串结果)和expr(将newFunc解析成表达式后的结果):
1 | //FuncFactor.java |
Definer
Definer类主要处理自定义函数的定义和调用。该函数的成员和方法都是静态的,无需实例化对象,直接通过类名即可调用。
-
Definer类有两个私有静态成员——funcMap和paraMap,两者都是HashMap类型:-
funcMap可以通过函数名(f/g/h)来获得函数的定义式; -
paraMap可以通过函数名来获得该函数的形参列表(x/y/z)。
-
-
Definer类还有两个函数——addFunc()和callFunc():addFunc()是在函数输入时使用,将终端输入的函数表达式传入该函数并进行解析,并将该函数的定义式和形参列表分别加入funcMap和paraMap;callFunc()是在函数调用时使用,传入的参量是函数名name和实参列表acturalParas,首先根据name获得函数定义式,再用replaceAll函数替换所有形参为实参。
1 | //Definer.java |
流程分析
迭代后程序依旧大致分为三个步骤——预处理、表达式解析、计算优化输出,下面进行具体分析与第一次作业的修改之处。
预处理
为了简化之后的步骤我的预处理增加了三个部分——
- 删除逗号后面无必要的+;
- 给每个逗号后面多加一个
(或,(目的是在处理praserFuncFactor()的时候,让每个因子都先转化为praserExpr); - 给逗号后面紧接着的
-前面加上0;
1 | //Processer.java |
【令小女子“伤春悲秋”的是,本次作业的强测我挂了一个点,bug是没在预处理的时候把“,”后面无用的+删掉,导致出现了“空指针”异常,所以细心非常重要,望引以为戒~】
表达式解析
表达式解析为了满足多层嵌套括号的要求,这里依旧选择递归下降算法,主要组成部分分别是——Lexer(词法分析器)和Parser(语法解析器)。
Lexer
在本次作业中语法单元的类型TokenType这一枚举类型新增SIN、COS、F、G、H、COMMA(逗号)。
1 | public enum TokenType { |
具体的Lexer实现如下:
1 | //Lexer.java |
Parser
-
为解析三角函数,我们在
parser类中设置了一个parserSinCosFactor()方法,该方法在parseFactor()中被调用。 具体解析的逻辑是:先将三角函数括号内的因子进行解析(即在该方法中再调用
parseExpr()方法),然后解析该三角函数的指数,最后将解析结果保存到一个SinFactor对象或者CosFactor对象中返回即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16//Parser.java
public Factor parserSinCosFactor() {
//...
Factor inside = parseExpr();
//...
if (type == TokenType.SIN) {
//这里因为TokenType已经多轮改变了,所以要额外用一个变量type存储下来
Factor sinFactor = new SinFactor(inside);
//指数处理
return sinFactor;
} else {
Factor cosFactor = new CosFactor(inside);
//指数处理
return cosFactor;
}
} -
为解析自定义函数,我们在
parser类中设置了一个parserFuncFactor()方法,该方法在parseFactor()中被调用。 具体解析的逻辑是:先按照函数的
name得到它形参的个数,然后解析该个数的实参(即在该方法中再调用parseFactor()方法),然后讲这个FuncFactor再次解析成Factor类型,最后将解析结果保存到一个newFuncFactor对象返回即可。1
2
3
4
5
6
7
8
9
10
11//Parser.java
public Factor parserFuncFactor(String name) {
//....
for (int i = 1;i <= (Definer.getParaMap().get(name).size()); i++) {
actualParas.add(parseFactor());
}
FuncFactor funcFactor = new FuncFactor(name,actualParas);
Factor newFuncFactor = funcFactor.getExpr();
//若有指数,读入分析
return newFuncFactor;
} -
PS:在这里回顾我们可以发现我在解析
sin、cos、f|g|h的括号因子的时候,前者用的parserExpr(),后者用的parserFactor(),这里实际上是一套配套的过程:- 对于
sin、cos的处理,我Lexer解析时pos+=4;,因此使用parserExpr(); - 对于
f|g|h的处理,我Lexer解析时pos+=1;,Processer中给,后面加上(,因此使用parserFactor()。
【没有固定的写法,所以可以根据个人的架构来选择构造哟~】
- 对于
计算优化输出
本次作业的计算单元通过分析可以归纳成式子——$$ax^n\prod_isin(Factor_i)\prod_jcos(Factor_j)$$
【这里小女子“被迫”花费了大量时间,尽是一把辛酸泪~】
Unit
Unit类就是原来的Mono类,改动最大的地方是——
- 建立
HashMap<Poly,Integer>的sinMap\cosMap;因为key是自定义类,因此hashCode()和equals()要按照自己的要求改动; - 为了后续的深拷贝,建立函数
public Unit cloneInSerializable()。
1 | //Unit.java |
Poly
Poly类和Unit类一样,改动最大的地方是——
- 建立
HashMap<Unit,BigInteger>的unitMap;因为key是自定义类,因此hashCode()和equals()要按照自己的要求改动; - 为了后续的深拷贝,建立函数
public Poly cloneInSerializable()。
1 | //Poly.java |
-
PS:本次大致可以优化性能的三个点:
- 合并所有的同类型;
- 转化
sin(0)=0、cos(0)=1; - 化简
sin\cos的因子(类似再同样的步骤进行一次小型MainClass),并判断删除无必要的括号,例如:sin((-1))=sin(-1).
【实际上,三角函数还可以用一些公式化简,例如:
sin(x)**2 + cos(x)**2 = 1、二倍角公式、积化和差公式等等,但是具体实现会拥有更多难度,小女子由于在debug上浪费了很多时间,所以并不曾有机会尝试化简~ 但经过“走访人世”,也听说了有很多同学尝试失败了,因此等待大牛留言~浇浇~】
第三次作业
本次作业需要完成的任务为:在上一次作业的基础上,增加求导因子,令自定义函数可以调用其他已经定义了的函数,共两项任务。
- PS:
- 求导仅仅包括
dx、dy、dz; - 更多要求详见教程
- 求导仅仅包括
UML类图

代码架构
数据结构
1 | Expr := Term | Term [+|-] Expr |
通过分析表达式结构,我们发现可以给Factor新增一种类——Term因子:
Term因子
只要把Factor接口接到Term上即可。
1 | //Term.java |
深拷贝
值得注意的是,在本次迭代代码的过程中,我使用了两种深拷贝的方式——序列化、重写clone():
序列化
使用序列化进行深拷贝的有两个类——Poly、Unit,使用序列化只要给该类加上接口Serializable,并编写函数cloneInSerializable(),以Unit类为例:
1 | //Unit.java |
重写clone()
使用重写clone()进行深拷贝的有七个类——所有使用了Factor接口的类,使用重写clone()只要所有涉及定义了变量的类都加上重写函数clone(),以Expr、Term、SinFactor类为例:
1 | //Expr.java |
流程分析
迭代后程序依旧大致分为三个步骤——预处理、表达式解析、计算优化输出,下面进行具体分析与第二次作业的修改之处。
预处理
本次我在预处理部分主要修改了两个地方——MainClass与Definer类:
MainClass
将语句定义到一个静态函数中public static Parser parserString(String str),方便在处理自定义函数定义部分来重复调用:
1 | //MainClass.java |
Definer
这一部分,我将处理自定义函数的定义式部分也当成了一次小型的表达式解析,来达到可以解决自定义函数中调用其他函数的问题:
【但是由于小女子自己代码架构的问题,这个部分被我自己埋下一个潜藏的bug,特导致强测又挂了一个点~ 哭唧唧~ 后续会有跟具体的分析】
1 | //Definer.java |
表达式解析
表达式解析为了满足多层嵌套括号的要求,这里依旧选择递归下降算法,主要组成部分分别是——Lexer(词法分析器)和Parser(语法解析器)。
Lexer
在本次作业中语法单元的类型TokenType这一枚举类型新增DX、DY、DZ。
1 | public enum TokenType { |
具体的Lexer实现如下:
1 | //Lexer.java |
Parser
-
为解析求导因子,我们在
parser类中设置了一个parserDerFactor()方法,该方法在parseFactor()中被调用。 具体解析的逻辑是:先将求导因子括号内的表达式进行解析(即在该方法中再调用
parseExpr()方法),然后解析该求导因子的指数,最后将解析结果保存到一个Expr对象返回。1
2
3
4
5
6
7
8
9
10
11
12
13
14//Parser.java
public Factor parserDerFactor() {
//...
lexer.next();
Expr inside = parseExpr();//注意按照表达式解析
lexer.next();
if (type == TokenType.DX) {
Factor dxFactor = inside.expand().derive("x");
Expr dxExpr = new Expr();
dxExpr.addTerm((Term) dxFactor);
//指数处理
return dxExpr;
} else //....
} -
通过观察上述的
parserDerFactor()方法,我们观察到最新增加并迭代的方法是expand()、derive(String),以下具体阐释这两个函数:-
expand()只有两个类中定义了
expand()函数——Expr、Term:PS:注意
other实例也是有符号的!!1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34//Expr.java
public Factor expand() {
for (int i = 0; i < terms.size(); i++) {
expr = Expr.mergeExpr(expr, (Expr) terms.get(i).expand());
//mergeExpr表示合并两个expr
}
//...
}
//Term.java
public Factor expand() {
// ...递归实现去括号
for (int i = 0; i < factors.size(); i++) {
Factor factor = factors.get(i);
if (factor instanceof Expr) {
hasExprFactor = true;
// ...other为其余因子组成的项
for (int j = 0; j < factors.size(); j++) {
if (i != j) {
other.addFactor(factors.get(j).clone());
}
}
//...
for (Term t : e.getTerms()) {
expr.addTerm(Term.mergeTerm(other, t));//实现乘法分配律
}
}
}
if (hasExprFactor) {
//...
} else {
//...
}
} -
derive(String)所有
Factor接口的类,都拥有derive(String)函数,以Expr、Term、CosFactor、PowerFactor类为例:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49//Expr.java
public Factor derive(String name) {
//...
for (int i = 0; i < terms.size(); i++) {
// ps:注意term求导会变成expr
expr = Expr.mergeExpr(expr, (Expr) terms.get(i).derive(name));
}
term.addFactor(expr);
// ...返回Term类型
}
//Term.java
public Factor derive(String name) {
//...
for (int i = 0; i < factors.size(); i++) {
Term t = (Term) factors.get(i).derive(name);
for (int j = 0; j < factors.size(); j++) {
if (i != j) {
// ps:乘法法则
t.addFactor(factors.get(j).clone());
}
}
//...符号处理
}
// ...返回Expr类型
}
//CosFactor.java
public Factor derive(String name) {
//...
term.addFactor(toSin());//toSin()如函数名字所表示,转为sinFactor
term.addFactor(new NumFactor(BigInteger.valueOf(-1), 1));
term = Term.mergeTerm(term, (Term) factor.derive(name));
// ...返回Term类型
}
//PowerFactor.java
public Factor derive(String c) {
if (base.equals(c)) {
//...
} else {
//...
}
// ...返回Term类型
}
-
-
PS:这里的逻辑操作,主要是借鉴了实验课的
exam2中对于求导的处理方式。【实验课真的很重要哇~ 疯狂爱上实验课提出的思路~ 好好听讲学习中】
计算优化输出
本次作业的计算优化部分我没有任何改动。【好的架构真的很重要哇~】
复杂度分析
最终版代码复杂度如下:
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| CosFactor | 1.0 | 1.0 | 7.0 |
| Definer | 2.5 | 5.0 | 10.0 |
| Expr | 1.6 | 3.0 | 16.0 |
| FuncFactor | 1.0 | 1.0 | 3.0 |
| Lexer | 5.166666666666667 | 13.0 | 31.0 |
| MainClass | 2.0 | 2.0 | 4.0 |
| NumFactor | 1.0 | 1.0 | 6.0 |
| Parser | 5.142857142857143 | 12.0 | 36.0 |
| Poly | 4.285714285714286 | 12.0 | 60.0 |
| PowerFactor | 1.6666666666666667 | 4.0 | 10.0 |
| Processer | 4.2 | 9.0 | 21.0 |
| SinFactor | 1.0 | 1.0 | 7.0 |
| Term | 2.6666666666666665 | 7.0 | 32.0 |
| TokenType | 0.0 | ||
| Unit | 2.5384615384615383 | 11.0 | 33.0 |
| Total | 276.0 | ||
| Average | 2.7058823529411766 | 5.857142857142857 | 18.4 |
其中有几个方法的复杂度格外高,是不足之处,也是有待优化之处:
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Lexer.next() | 23.0 | 2.0 | 12.0 | 17.0 |
| Parser.parseFactor() | 20.0 | 6.0 | 17.0 | 18.0 |
| Poly.printCos(StringBuilder, Unit) | 20.0 | 4.0 | 14.0 | 14.0 |
| Poly.toString() | 24.0 | 3.0 | 17.0 | 18.0 |
| Processer.adjustSign() | 14.0 | 3.0 | 10.0 | 13.0 |
| Processer.delPlusMinus() | 16.0 | 3.0 | 6.0 | 10.0 |
| Term.expand() | 15.0 | 4.0 | 7.0 | 7.0 |
| Unit.mulUnit(Unit) | 20.0 | 1.0 | 11.0 | 11.0 |
| Total | 320.0 | 138.0 | 297.0 | 337.0 |
| Average | 3.1372549019607843 | 1.3529411764705883 | 2.911764705882353 | 3.303921568627451 |
强测互测分析
强测
第一单元我强测一个挂了两个点,分别在第二次作业和第三次作业各一次。其中,第二次作业的bug是因为预处理中少了一个去除加号的判断条件,与代码架构关系不大,这里不具体分析。
但是,第三次作业的bug与代码架构有千丝万缕的联系,这里具体分析一下:
在我的代码架构中,处理自定义函数的时候,为了准确读取分析好各个实参,我在所有的逗号后面加了一个(,以便于在读取实参的时候,能够强制转化成Expr类型,才能使我的代码正确处理实参中外嵌乘方的形式。
而第三次作业中,我的问题便出现在这里,我的错误代码在读入处理自定义函数定义式的时候,进行了两个遍预处理,于是导致自己的所有的逗号后面加了两个(,导致parserFunctor()中读取实参的时候无法准确确定实参的结尾,故而导致的bug。
实际上,这个bug可以看做是一种由于偷懒【唉声叹气ing,又又又又又又被懒惰偷袭了~】导致的双层预处理错误,但是我仔细思考之后,认为这可以看做我代码架构的问题:在解析实参的时候用的parserFactor(),而不是parserExpr(),如果直接按照表达式处理,虽然会导致我要改动parserExpr()方法中的部分逻辑结构,但可以避免我上述所犯的错误。
互测
评测机的重要性!!在互测的时候实际上也是在同步进行OS课程的实验任务,因此hack别人的时间是十分有限的,如果一个个仔细研究互测成员的代码,时间会明显不足够。因此,这里我推荐的hack别人的方法是:先用评测机确定大致有问题的代码方向,然后带有指向性地阅读成员代码,来寻找bug的原理,据此编写待提交的hack数据。
后记
第一单元的学习总的来说还是相对比较难的,难度主要在从无到有的创造感、迷茫感与突破性。同时,通过各项数据的对比,我们也清晰地了解到OO先导课的重要性和不可取代性。参考借鉴往届学长学姐的Blog将会是一项十分有用的助力。


